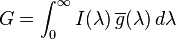色度學(不是很正確,只是筆記的整理)
¶色度學(不是很正確,只是筆記的整理)
原文連結: https://darkblack01.blogspot.com/2012/08/blog-post_29.html
移植時的最後更新日期: 2012-11-22T11:41:07.867+08:00
顏色的認識與詮釋
對於顏色的認識,從看見可見光,開始認識顏色
對於顏色的詮釋,從下面各種方式,從低精確度到高精確度
概括→通用定義→色卡→辨識直覺→物理定義
那如何量化顏色?
這個問題開啟了從光譜學出來的另一個分支色度學。
(歷史的脈絡也是這樣的嗎?)
顏色,是一種電磁波經人體編解碼而產生的效果。所以,可以說是 輻射學+人眼=色度學 可以由光譜學+人眼限制條件去看色度學
顏色產生:
背景光源×反射物×人眼感受
顏色參數:
亮度:顏色強度(和透明混合的程度)(振幅)
飽和度:成份(和白色混合的程度)(光譜雜訊)
色相:各色混合的程度(波長)
第一個實驗:
在光度學中,定義光度函數(視見函數),不同於輻射度量學,不考慮人眼敏感度。
(那…也就是說若固定人眼敏感度(只看單一波長的光)就可以參考輻射度量學?)
 |
x軸:波長,y軸:百分比,人眼對各波長敏感度的相對比例。 (只是不知道圖中的綠線、實線、點線和虛線各有什麼差,實線為人眼) |
第二個實驗:
顏色匹配實驗:定義基礎顏色和人眼的敏感度
問題:什麼是基本顏色?
色彩學的故事跟我們說,以前的人對於這件事的討論和實驗,有了一個結論,就是RGB。
儘管亞里士多德就已經討論過光和顏色之間的關係,但真正闡明兩者關係的是牛頓。歌德也曾經研究過顏色的成因。托馬斯·楊在1801年第一次提出三元色的理論,後來亥姆霍茲將它完善了。1960年代人們發現了人眼內部感受顏色的色素,從而確定了這個理論的正確性。
人眼中的錐狀細胞和棒狀細胞都能感受顏色,一般人眼中有三種不同的錐狀細胞:第一種主要感受黃綠色,它的最敏感點在565奈米左右;第二種主要感受綠色,它的最敏感點在535奈米左右;第三種主要感受藍紫色,其最敏感點在420奈米左右[1][2]。桿狀細胞只有一種,它的最敏感的顏色波長在藍色和綠色之間。
對於認知科學中的顏色認識,可以看另一篇《色彩繽紛的世界》
經過實驗訂出來 顏色-敏感度曲線
x軸:波長,y軸:百分比,人眼錐狀細胞對各波長敏感度的相對比例。 |
以下轉錄自維基百科《CIE1931色彩空間》
觀察者改變三種原色光的明度直到觀察到混合的顏色匹配了測試顏色。不是所有顏色都可使用這種技術匹配。當沒有匹配的時候,可變數量的一種原色被增加到測試顏色上,用餘下兩種原色混合與它匹配。對於這種情況,增加到測試顏色上原色的數量被認為是負值。通過這種方式,可以覆蓋完整的人類顏色感知。當測試顏色是單色的時候,可以把使用的每種原色的數量繪製為測試顏色的波長的函數。這三個函數叫做這個特定實驗的「顏色匹配函數」。
為什麼選RGB?
選擇波長 546.1 nm 和 435.8 nm 的原色是因為它們是容易再生的水銀蒸氣放電的色線。
1931 年選擇的 700 nm 波長難於再生為單色光束,選擇它是因為眼睛的顏色感知在這個波長相當不變化,所以在這個原色波長上的小誤差將對結果有很小的影響。
| 顏色匹配函數 使用RGB三種顏色的合成,可以涵蓋所有人眼感知的光譜。 |
經過 CIE 的特別委員會的深思熟慮之後確定了顏色匹配函數和原色(Fairman 1997)。在圖的短波和長波的側的取捨點某種程度上是隨意選擇的;人類眼睛實際上能看到波長直到 810 nm 的光,但是敏感度要數千倍低於綠色光。定義的這些顏色匹配函數叫做「1931 CIE 標準觀察者」。注意勝過指定每種原色的明度,這種曲線通常規範化為在其下有固定的面積。這個面積按如下規定而固定為特定值
結果的規範化顏色匹配函數經常對源照度按 r:g:b 比率 1:4.5907:0.0601 縮放、和為源輻射功率按比率 72.0962:1.3791:1 縮放來重新生成真正的顏色匹配函數。通過提議標準化原色,CIE 建立了客觀顏色表示法的一個國際系統。
得到「Wright–Guild 數據」
加上「Grassmann 定律」
這些都是內積,並可以被認為是無限維頻譜到三維顏色的投影。
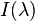 為該光束對波長的強度分佈;
為該光束對波長的強度分佈; ,
, ,
, 則分別為人眼中三種錐狀細胞對不同波長的反應強度。
則分別為人眼中三種錐狀細胞對不同波長的反應強度。制訂 CIE XYZ色彩空間
感覺一直在抄維基!XD
之後利用座標轉換,使x座標不再出現負值(但是我認為這個論點不是很有力,應該有其它別的原因,才有可能轉換座標)
成為了最後的CIE 1931
之後因為色均勻度的問題,再繼續發展其色度圖。
問題:
x, y相加減的值≠顏色差異程度
 |
| 轉貼自 http://www.chromapure.com/colorscience-dE.asp |
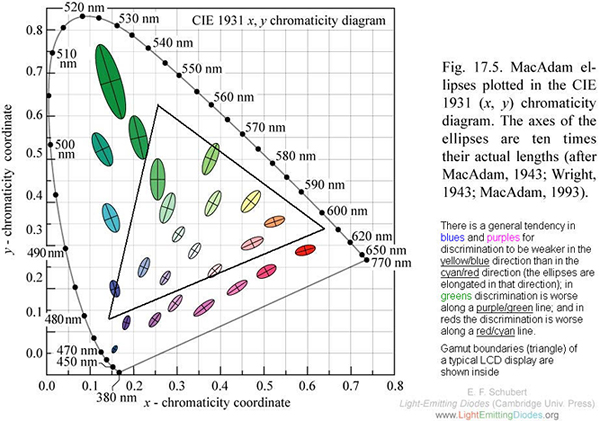 |
| 轉貼自 http://www.marcelpatek.com/images/MacAdam1.jpg |
也因為這個問題,出現了孟塞爾色彩空間,它就是均勻分佈的顏色。
但是其缺點是無法量化表示,所以一直沒有被拿來使用。
但是,1931卻已廣為流傳,所以之後的色度圖都畫回了1931
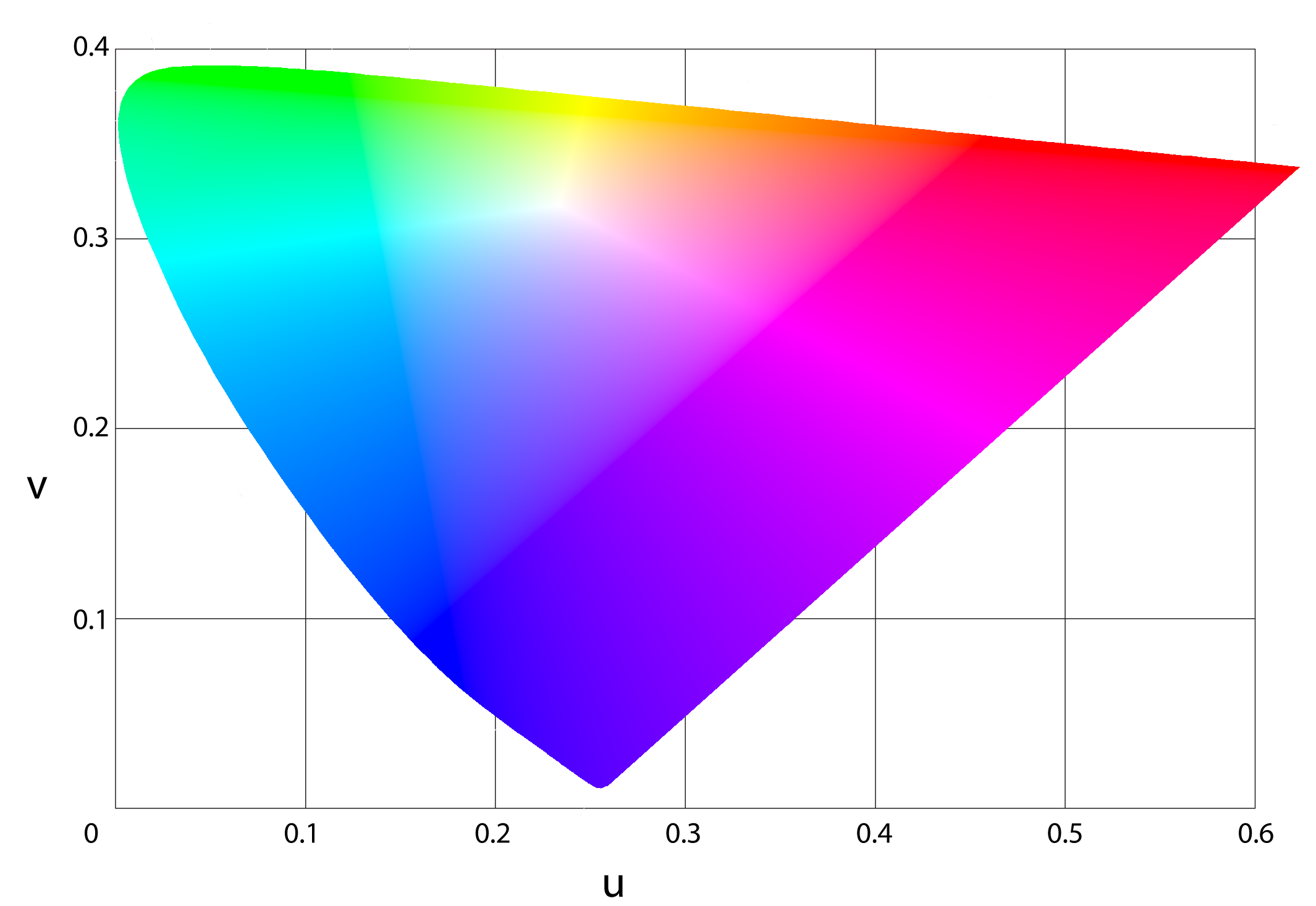 |
| 色度圖的均勻顏色版本 |
但是,1931卻已廣為流傳,所以之後的色度圖都畫回了1931
 |
| 轉錄自 http://www.nanocotechnologies.com/content/ Library/CaseStudies/articles/Creating_warm_white_ light_with_quantum_dots_QDSSL/23.aspx |
 |
| 轉錄自 http://www.ledct.cn/jishu/cie.htm |
發表於
tags:
{ 社大的日子 }
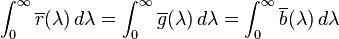
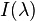 的一個顏色的 RGB
的一個顏色的 RGB