除了這個方程式，還有一個數列要介紹，就是節點向量(knot vector)

要得到節點向量必須要有兩件已知：

定義t0、t1、t2、t3、t4、t5…、t(n+k+1)的值如下:

我們先看懂節點向量表達的東西，在此還無法全面的解釋其意義。

它可以得到

其定義域為u: [0, (n+1)-k]

基底函數的值皆由此取值運算得到。

基底函數
(basis function or blending function)

主方程式除了控制點座標就是這個鬼東西了！這也是整個方程式中最不好看懂的部份。
原因在於它的遞迴關係。
定義：

上式是遞迴關係，下式是遞迴終端該是什麼值。 在此終端也是判斷出來的，並不是運算出來的。

上式的遞迴關係，這樣看有點小複雜，讓我們把式子「攤開」來！

我們先試著把遞迴完的式子代進來，發現遞迴到最後，式子會由兩個部份組成

1. u和節點向量的數字t
2. 下一層的Ni,k

由於k會一直-1，所以式子會一直到k=0的時候，直接由基底函數的另一個定義Ni,0來判斷該代多少數字，而決定這個判斷的參數，是u和節點向量t
可以看見，在每一層的k和i的變化。

在k=0, 遞迴出來的索引值最多不會超過節點向量的範圍 (total: (n+k)+1, 最後一個值的索引為t(n+k) )

整個基底函數的式子，會如下：

T0(u)是k次方的運算式，隨著i遞增，k也會改變。

基底函數的判斷條件，就由Ni,0的定義決定。

ex:
因為k的關係，節點向量的頭尾都會有一段，值都相等，所以靠近N0,0和N0, n+k都會等於0，只有中間的值會等於1(有值)，而中間會有幾個區間為有效(N0,k=1)，但是邊界條件各有不同。

運算範例

看到這，有點花花厚？！
來試算一下吧！

我們拿參考資料[1]的例子來精算一次。
設k=2, n+1=5

節點向量如下

下圖，是依「定義域、值域」分成三大色塊，黃色值域為0，藍色的值域為最大值n+1-k，紅色則是其它平均分佈的中間值。

最上面是節點向量與索引值的值域定義。 最下面是節點向量的值與索引值的內容。 中間是節點向量的分佈圖。

基底函數如下

將節點向量的值直接代入t0~t7
定義0≦u≦3, u為實數(有小數點的)


在此例中，基底函數的最後五個函數，畫出來如下圖(圖中k=2, n=4(5個控制點))

圖片來自：張家源，B-Spline 有限元素法解三維彈性力學問題，碩士論文，國立成功大學機械工程學系，台南(2008)[1]

x軸是我們的u，也就是定義域。
y是基底函數輸出的值。

注意:
幾條線就是幾個控制點×基底函數(N0,k~Nn,k)。
如果k等於n，那就是貝茲曲線了

最後把全部的東西，通通代入原式

依Ni,0的各個邊界條件整理一下式子，如下：
式子要表達的如下：
變動P0，第3式和第2式的曲線不受影響。
變動P1，第3式的曲線不受影響。
變動P2，全部都受影響。
變動P3，第1式的曲線不受影響。
變動P4，第1式和第2式的曲線不受影響。

f(x)=PB-spline(u)的意義，是一個點，定義在2維空間中p(x,y)


最後呈現出來的就像這樣，控制點沒有在曲線上面(像貝茲曲線這樣)

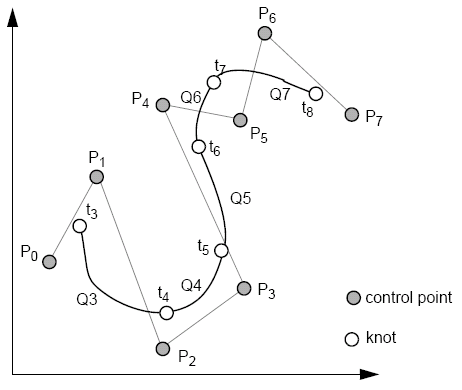圖片來自: Computer Graphics and Visualisation[2]

參考資料:
[1] 張家源，B-Spline 有限元素法解三維彈性力學問題，碩士論文，國立成功大學機械工程學系，台南(2008)
[2] Computer Graphics and Visualisation